This is my second post on UMD CS’s programming languages course, CS 330.
We introduce Ruby and OCaml as exemplars of dynamic/scripting and functional languages, respectively, in the first half of the course. I described these in the first post. This post covers the third quarter of the course. This part goes over technologies that underpin a language’s design and implementation, in particular regular expressions, finite automata, context-free grammars, and LL-k parsing. It also looks at the lambda calculus as a core model of computation, and operational semantics as way of precisely specifying what programs mean. The last part of the course discusses the basics of software security and coding strategies for avoiding various vulnerabilities. I will dedicate a separate post to these last topics.
I’m very curious for your feedback on the course overall. I welcome suggestions for improvements/adjustments to the content!
Formal Languages
Regular expressions and formal grammars are ubiquitous concepts in computer science. They are used to define packet layouts, file formats, and communication protocols. They are also at the heart of most programming language implementations. Regular expressions are used to define a language’s scanner (aka lexer), which breaks a source file into a stream into tokens, such as numbers, identifiers, keywords, punctuation, etc. Context-free grammars (CFGs) are used to define a language’s parser, which consumes the stream of tokens and confirms they consistute a sensible program. In the process, the parser produces an abstract syntax tree (AST), which is the object of further processing and the basis for ultimately executing the program, whether by interpretation or compilation.
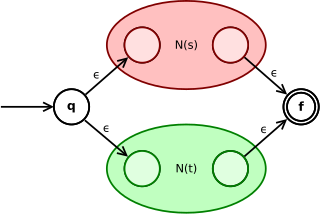
A non-deterministic finite automaton
In 330 we explore the basics of formal language theory. We show how regular expressions “compile” to non-deterministic finite automata (NFAs) and how these in turn can be converted to deterministic finite automata (DFAs). We informally close the loop by stating (but not proving) that DFAs map to regular expressions — a beautiful, classic CS result. We also explore the formal definition of a CFG and how to build (when possible) a recursive descent parser for one. Two of our programming projects involve these topics. One asks students to implement the RE ⟶ NFA ⟶ DFA mapping, and thereby produce a regular expression matcher. The other asks them to build an interpreter (including its lexer and parser) for a “small C” language.
Rationale
I believe that 330 is unusual in that these topics tend to show up in other CS courses, not in the “PL course.” Formal languages often appear (in greater depth) in a theory of computation course, among other theoretical topics (CS 452 at UMD). Parsers often only appear in a compilers course (CS 430). At UMD, neither of these other courses is required, so 330 might be a student’s only exposure to these topics. I think that this exposure is useful. These are important, general topics, and 330’s presentation of them points the way for interested students to dig deeper, in later courses, if they like.
Operational Semantics
Having introduced two new programming languages to students in the first half of 330, we step back and ask students to reflect: What just happened? You didn’t know OCaml before, and now you do. How did we explain it to you? Mostly we used English prose and examples. This is the norm for most programming languages, which are, at best, specified in a careful, expository document, and at worst (or in addition) “specified” by the behavior of their canonical compiler/interpreter implementation.

Operational Semantics Rules (Small C)
But this approach is unsatisfying, because English can be ambiguous. Corner cases hard to interpret and lead different implementations of a language to disagree. As such, a formal, mathematical presentation is preferred. In 330, we introduce students to operational semantics. While other styles of formal semantics have also been developed, operational semantics is relatively simple and has evolved into an intuitive and comprehensive mechanism. As a ready application, we use operational semantics (and prose) to specify the “small C” language for which they must write an interpreter in OCaml.
Approach
When I first learned formal semantics as a graduate student, I found it hard to grasp. Semantics is not inherently difficult, but I lacked concepts to which to relate the ideas and notation. In anticipation that might students might struggle similarly, 330 tries to draw several connections while leading up to the ultimate, formal presentation.
First, we lay the groundwork when teaching OCaml. The lectures present OCaml semi-formally, on a per-feature basis. For example, see slides 2-4 of this lecture, which show let-binding expression forms as syntax, evaluation semantics, and typing. When specifically presenting operational semantics, we revisit this notation and presentation style, but focus on details we had previously elided, e.g., the use of grammars, metavariables, keywords, etc. We also map the pedantic style of the prose we used for OCaml to equivalent, formal operational rules. For example, in the operational semantics lecture‘s slides 11-12 we define the big-step semantics judgment e ⇒ v which is read “e evaluates to v”. Then we give the semantics of a simple expression language in idiomatic prose. Then in slides 13-15 we show how that prose can be written more concisely in the form of logical rules of inference.

An interpreter and the corresponding inference rules
As a second connection, we relate operational semantics to an interpreter. We explain how the formal expression language is like an OCaml datatype, and the operational inference rules can be transliterated into a recursive function over (OCaml) values of that datatype. Derivations according to the rules of inference map fairly directly to the recursive call structure of the interpreter. See slides 20-21. The rest of the lecture extends the core language, presenting rules (and interpreter code) for the added features. It also introduces type checking, showing it follows a similar style. When presenting CFGs, we connect the formal notation for defining the language as an AST (here) to a CFG. This way, students can see how a parse might be built for an interpreter implementation.
Assessment
I am pretty happy with this pedagogical approach. Whereas students did relatively poorly on quizzes and exams in the past, the general performance has gone up to the level of other course topics. My impression is that students with a real interest in this material understand what’s going on more deeply, too. It sets them up nicely for a more detailed presentation of semantics in our compilers class, or our graduate-level programming languages class. (I had five undergrads take the grad class in Fall’17, and they all did really well, with several going on to grad school.)
Lambda Calculus
Operational semantics naturally points the way to formal presentation of the lambda calculus as a core, mathematical model of computation. Most students have heard of Turing Machines, and know they are a core formalism for computability. Few know that Church‘s lambda calculus is equally powerful. Moreover, while Turing machines follow a low-level, imperative style of programming, lambda calculus follows a high-level, functional style. As such, it is a good topic for 330 following our presentation of OCaml.
We spend two lectures on lambda calculus. The first is on the basics — motivation, syntax, and semantics. As with operational semantics, we provide some conceptual grounding by connecting the lambda calculus syntax to an OCaml data type and its single-step reduction semantics to an interpreter (also written in OCaml). Much of the lecture is spent covering the nuances of “parsing” and substitution.

Lambda Calculus Church Numerals
The second lecture works through an informal argument for why lambda calculus is Turing complete. It shows basic encodings for booleans, tuples, natural numbers, and looping via a fixed point combinator. With these, we can write code we are used to expressing in high-level languages. This is a pretty fun illustration of the power of abstraction. Numbers and arithmetic have a certain semantics, and whether you implement those as twos-complement bit vectors or as lambda terms doesn’t matter — from the “outside” the program using those numbers can’t tell the difference.[ref]Technically speaking, this equivalence would require using modular arithmetic with our Church numerals.[/ref] We close by pointing out that types are easy to add to the lambda calculus, but that adding them can compromise Turing completeness.
Other Stuff
Throughout the course we draw several other connections between programming languages. We talk about type safety, and especially what it means for static vs. dynamically typed languages (I draw on Robert Harper‘s argument from his text that dynamically typed languages are really “uni-typed”). We talk about the connection between objects and closures. We also talk about objects and abstract data types (ADTs), following William Cook’s essay. And we talk about tail recursion and its connection to loops. I would have liked to talk about continuation passing style, but we ran out of time this semester. We also have fun going over the history of programming and programming languages on the last day of class.
Summary
CMSC 330 aims to expose students to a breadth of programming languages concepts, to improve their understanding of different languages and problem solving styles. While much of the course is hands-on, involving programming with particular languages like Ruby, OCaml, and Rust, a substantial part is also mathematical/conceptual, introducing students to formal language theory (underpinning language implementations), lambda calculus, and operational semantics. We also make close connections between different styles of language, identifying costs/benefits.
My final post on 330 will consider a recent change to the course that covers software security, and the role the Rust programming language plays in achieving it.

Pingback: Teaching Programming Languages - The PL Enthusiast
Pingback: Software Security is a Programming Languages Issue - The PL Enthusiast
https://racket-lang.org/ 😉
Pingback: Re-Imagining the “Programming Paradigms” Course | SIGPLAN Blog