In my last post, I summarized some of the topics and problems considered at a recent Dagstuhl seminar I co-organized on the Synergy between Programming Languages and Cryptography. The post surveyed how programming languages often interface with cryptography in the construction of secure systems, and in particular how they can make it easier to implement cryptography, use it, or verify its correctness.
Beyond using PLs as a tool for easier/safer use of Crypto, there is an opportunity for certain kinds of thinking, or reasoning, to cross over fruitfully between the PL an Crypto communities. In particular, both communities are interested in formalizing systems and proving properties about them but they often use different methods, either due to cultural differences, or because the properties and systems of interest are simply different. During the workshop we identified both analogous, similar styles of reasoning in two communities and connection points between the different styles of reasoning. In this post I briefly highlight a few examples of each, and point to future research opportunities.
Analogies between PL and Crypto Reasoning
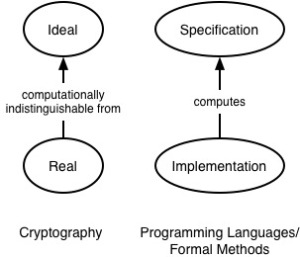
One observation we made during the workshop is that the now-standard Ideal/Real paradigm for proving security in Crypto matches the Specification/Implementation connection in formal verification of software. As shown the following diagram, we can view the Ideal as a specification, and the Real as like its implementation.
The Ideal/Real paradigm was first proposed by Goldreich, Micali, and Widgerson in their work on Secure Multiparty Computation (SMC), and further developed by Canetti in his universal composability (UC) framework.[ref]It’s debatable whether this paradigm was in fact developed even earlier, in conjunction with ideas about zero knowledge proofs.[/ref] The basic idea is to treat a cryptographic computation among parties as if it were being carried out by a trusted third party (the “ideal”), and then prove that the actual implementation (the “real”) emulates this ideal, in that the parties can learn nothing more than they would in a protocol involving a trusted party. (The paradigm also handles correctness, robustness, and other emergent properties.)
This is a classic kind of abstraction also present in formal verification: If a program P uses a module M that implements specification S, then relinking P to use M’, which also implements S, should preserve the correct execution of P. One talk, by Alley Stoughton, made the interesting observation that the Real/Ideal notion might be a suitable organizing principle around which to verify software is secure, essentially by using the Ideal as a richer kind of security property than is typical in PL (which often looks at properties like information flow control), and using abstraction in key ways to show it is enforced.
In the Crypto setting, the Real-to-Ideal connection is established probabilistically, considering a diminishing likelihood that a computationally bounded adversary would be able to tell the difference between the Real and Ideal. In the PL setting, the specification-implementation connection is established using methods of formal reasoning and logic, and usually without considering an adversary.
However, a notion of adversary does arise in PL-style reasoning. In particular, an adversary can be expressed as a context C[∙] into which we place a computation e of interest that is subject to that adversary; the composition of the two is written C[e]. One PL property in this setup with a Crypto connection is contextual equivalence, which states that e and e’ are equivalent iff for all contexts C the outcome of running C[e] is the same as running C[e’] — e.g., both diverge or evaluate to the same result. In a PL setting this property is often of interest when proving that two different implementations of the same abstract data type have the same semantics (in all contexts). In a security setting we can view the contexts as adversaries, and e and e’ as the Real and Ideal.
Another useful property is full abstraction. This property was originally introduced to connect an operational semantics to a denotational semantics — the former defines a kind of abstract machine that explains how programs compute, while the latter denotes the meaning of a program directly, in terms of another mathematical formalism (like complete partial orders). Both styles of semantics have different strengths, and full abstraction connects them: it requires that e and e’ are observationally equivalent (according to the operational semantics) if an only if they have the same denotation (according to the denotational semantics).
In a Crypto setting, we might view the operational semantics as the Ideal and the denotational semantics as the Real, and full abstraction then states that despite the added observational power of the Real setting, an adversary cannot distinguish any more programs (i.e., learn any additional information) than he could in the Ideal setting. As a recent example of its use, Abadi and Plotkin used full abstraction to reason about the effectiveness of address space randomization. Another recent result is a fully abstract compiler from a type-safe high-level language to Javascript; the compiler effectively defines the denotational semantics, and the fact that it is fully abstract means that the added adversarial power that Javascript provides cannot violate the source language’s semantics. (The linked page provides an interesting primer and tutorial on fully abstract compilation.)
Connections between PL and Crypto Reasoning
The seminar also brought out ways that PL-style reasoning can be connected to Crypto-style reasoning for stronger end-to-end assurance of security. One connection point was at the Real/Ideal boundary. In particular, for privacy-preserving computation (or computation preserving some other security property), Crypto-style reasoning can first be used to establish that the Real emulates the Ideal, and then PL-style reasoning can consider the security of the Ideal itself.[ref]Here we are proposing to compose (or connect) PL-style reasoning about the Ideal with Crypto-style reasoning about the Real; in the previous section we pointed out that both kinds of reasoning have some similarity, e.g., PL-style proof of implementation satisfying specification, and Crypto-style proof of Real simulating Ideal.[/ref]
For example, consider the setting of SMC. Here, we have two (or more) parties X and Y that wish to compute a function F of their inputs x and y, whereby each party only learns the output F(x,y), but does not “see” the inputs. That is, the security goal is to establish that the Real computation of F(x,y) is indistinguishable from the Ideal model of executing F at a trusted third party. While Crypto can establish that a technique like garbled circuits effectively emulates a trusted third party, it does not establish that the output of F, even when computed by the Ideal, does not reveal too much information. For example, if F(x,y) = y then X learns Y‘s value y directly. More subtly, if F(x,y) = x > y, then if x = 1, an output of TRUE tells X that Y‘s value y = 0. PL-style reasoning can be applied to functions F to establish whether they are sufficiently private, e.g., by using ideas like knowledge-based reasoning or type systems for differential privacy. PL-style reasoning about knowledge can also be used to optimize SMCs by identifying places where a transformation would not affect security (e.g., no more is learned by an adversary observing the transformed program), but could improve performance.
Another way to connect PL to Crypto is to factor security-sensitive computations into general-purpose and cryptographic parts. Then PL-style methods can be used to specify the overall computation with the Crypto parts carefully abstracted out. The proof of security then follows a PL approach, assuming guarantees provided by the Crypto parts, which are separately proved using Crypto techniques. In a sense we can think of the PL techniques as employing syntactic/symbolic reasoning, and the Crypto techniques employing computational/probabilistic reasoning.
This is the approach we took our LambdaAuth work on authenticated data structures, in which the key idea involving the use of cryptographic hashes was abstracted into a language feature, and the proof of security combined a standard PL soundness proof along with a proof of the assumption that hash collisions are computationally difficult to produce. Recent work by Chong and Tromer on proof-carrying data similarly considers a language-level problem and proves useful guarantees by appealing to abstracted cryptographic mechanisms. Likewise, work on Memory Trace Obliviousness reasons about Oblivious RAM abstractly/symbolically in a PL setting to prove that the address trace of a particular program leaks no information.
What next?
I hope this post and the previous one give you some ideas for how PL and Crypto can put their heads together to produce interesting and useful results. I think there are many more opportunities to find possible connections. Here are some (less than) half-baked ideas:
- The question of composability comes up in both Crypto and PL: Can we take two modules that provide certain guarantees and compose them to create a larger system while still ensuring properties proved about each module individually? Each community has notions for composability that are slightly different, though analogous, as discussed above. Can we make precise connections so as to bring over results from one community to the other?
- Crypto currencies, exemplified by BitCoin, are an area of exploding interest. An interesting feature about these currencies is that they provide a foundation for fair, secure multiparty computation, as demonstrated by Andrychowicz, Dziembowski, Malinowski, and Mazurek in their best paper at IEEE Security and Privacy ’14. Could PL-style reasoning be applied to strengthen the guarantees provided by such computations?
- Cryptographic properties are often proved by making probabilistic statements about a system subject to a computationally bounded adversary. Could program analyses be designed to give probabilistic guarantees, drawing on the connection between adversary and context mentioned above, to thus speak more quantitatively about the chances that a property is true, or not, given the judgment of an analysis? How might random testing, which has proved highly useful in security settings, be reasoned about in a similar way?
Thanks again to the participants of the seminar; it was a great week that presented many new ideas to think about!

Pingback: The Synergy between Programming Languages and Cryptography - The PL Enthusiast