This post is the second part of a post on using ideas from programming languages to assist the design of authenticated data structures (ADSs). I will describe a small programming language extension for building ADSs that I co-developed with Andrew Miller, Jonathan Katz, and Elaine Shi, called LambdaAuth. A paper on this language was presented at POPL’14 and the implementation is freely available.
As a word of warning, this post goes into some technical detail. The goal of doing so is to make, in detail, a general point: programming language researchers’ focus on ways of programming (often embodied as language features, patterns, transformations, or analyses), rather than particular programs, yields broadly applicable results, extending outside of the motivating examples or domain. In this case, LambdaAuth embodies a simple mechanism for programming any authenticated data structure, not just one particular kind.
If you get bogged down in the details, you can always jump to the Conclusions at the end, which elaborates on this main point.
Authenticated Data Structures
The original post introduced the idea of an ADS. To recap, briefly: An ADS supports outsourcing data management tasks. A server stores a data structure and performs operations on that data structure requested by a client. To assure the client these outsourced operations have been performed correctly (i.e., they are “authentic”), the server provides a proof along with the result. An ADS is secure if the server can successfully lie about the result only with negligible probability. It is correct if the result is the one you would get from using a “normal”, non-authenticated version of the data structure.
Security and correctness of an ADS written in our language LambdaAuth follows from type correctness, which is relatively easy for the programmer to ensure. Conversely, the previous state of the art required the programmer to produce security and correctness proofs for every ADS they developed. LambdaAuth‘s design helps to isolate the key elements involved in the security of the ADS so that they can be proven effective once and for all, rather than on a per-data structure basis.
Example: Binary Search Tree
Suppose the outsourced data structure we are interested in is a binary search tree (BST). Creating an authenticated BST in LambdaAuth is as easy as writing an ordinary BST in OCaml. The following code (adapted from examples/bintree.ml in our distribution) is an example of membership lookup, where the tree stores integers:
type tree = Leaf | Node of (tree * int * tree) authtype
let rec (contains : int -> tree authtype -> bool) x t =
match t with
| Leaf -> false
| Node a -> let (l,y,r) = unauth a in
if x = y then true else if x < y
then contains x l
else contains x r
Ignoring the authtype type operator and the unauth keyword (imagine just erasing them from the code), this is a standard binary search tree. In short: trees are either a Leaf (which has no data associated with them) or a Node consisting of two sub-trees and an integer value. The contains function takes two arguments, an integer x and a tree t and returns whether t contains x. If the tree is a Leaf then it contains no values, much less x, so the answer is false. If the tree is a Node, then the function compares x against the value y stored at that node, returning true if they match, or else recursing to the left sub-tree if x < y and the right sub-tree otherwise.
Client and Server Code
The LambdaAuth compiler automatically generates executables for both the client and the server from this single piece of input code. For normal language constructs, compilation proceeds as normal, and both parties get the same code. The interesting part is the added syntax.
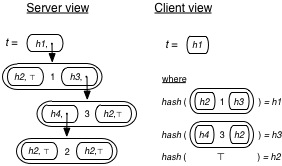
Data of type ‘a authtype is represented at the server as a pair consisting of a value of (the server representation of) type ‘a, and a cryptographic hash (e.g., using SHA1) of a shallow projection of that value, which is a serialized version of the representation of that value up to and including, but not beyond, any nested hashes. We will write hash(v) to indicate taking the cryptographic hash of the serialized (i.e., flat byte) representation of v. At the client, ‘a authtype values are only the hash, and not the value. This is how ADSs are used for outsourced storage: The server’s view of the tree is the entire data structure (starting at the root, which is the tree and its hash), while the client’s view is just the root’s hash.
As an example, the following picture shows the client’s and server’s view of the same tree, which has type tree authtype (that is, it is a tree whose root is also authenticated). Leaf elements are depicted as ⊤, and Nodes are depicted as the large ovals. The lower right of the figure shows how h1, h2, etc. are computed as the hashes of the shallow projections of corresponding tree elements.
Returning to the code: The unauth keyword is a function that takes a value of type ‘a authtype and returns a value of type ‘a. At the server, a value of type ‘a authtype has form (h,v) where h is the hash and v is the value. unauth will return v (which has type ‘a), and at the same time it will add the shallow projection of v, call it sp(v), to the current proof, which will consist of a list of shallow projections. Importantly, recall that h = hash(sp(v)). The complete proof is sent to the client, along with the final answer.
To verify the authenticity of the server’s answer, the client runs its version of the code on its version of the data (e.g., starting with the root hash), consuming the server’s proof. Each time the client reaches an unauth, the provided argument will simply be a hash value h. At the client, the unauth function will pull the front element from the proof stream (call it s), compute its hash (call this h’), and confirm that h = h’, returning s, if so. Recall that s should be the shallow projection of the actual value in the tree, so it will have the “shape” assumed by the current computation. Importantly, the fact that the client’s hash h matches the hash h’ of this shallow projection, means that this shallow projection is correct one, with high probability. The reason is that hash functions are “one way,” in the sense that it is very hard to find a value v such that, for a given h, hash(v) = h.
Example Execution
Returning to our example, the client could ask the server to compute (contains 4 (unauth t)); that is, whether the tree contains the integer 4. The answer will be false, producing the following proof stream:
The first element comes from the first call to unauth, which is applied to the initial tree. The shallow projection of the root’s value is added to the front of the proof stream (the leftmost value). Notice that the shallow projection includes the data in the root node, and the hashes of the subtrees, but not the values of the subtrees. The next element of the proof comes from a recursive call to contains, which is given the right subtree. The unauth call puts its shallow projection in the proof. The final element is just a Leaf which is due to the last recursive call; the shallow projection of a non-authtype-containing value is just the value itself.
The client will run its version of the code to consume this proof. On the first call (contains 4 (unauth t)), the t that is passed in is the root hash h1. The client will dequeue the first element of the proof and compute its hash. As shown in the first figure above, the hash of this element is h1, so hashes match and we can proceed computing with the shallow projection as the returned value. The recursive call will pass h3 as the tree argument, and the subsequent unauth call will compute the hash of the second element of the proof. The hash is h2, as shown in the first figure, so once again the hashes match. The final call is to the leaf, so the element is not in the tree, and false is returned.
Why does it work?
Congratulations on making it this far! Now that you have seen a LambdaAuth example, let’s step back and reflect on why it works.
The key idea in LambdaAuth is that it can use a root of trust, the initial hash, to extend trust to data (the shallow projections) provided in the server’s proof, ultimately reproducing the entire computation. Doing so makes sense because hashes are recursive, covering all of the data below them, including the nested hashes, but not the data that those hashes themselves cover. The server’s proof begins with the data covered by the initial hash that the client trusts, i.e., the shallow projection of the root of the tree. In confirming that the hash is correct (by recomputing the hash from the data and comparing it to the client’s own hash), the client extends its trust to the given data, including the nested hashes. It can therefore compute with that data safely and use any nested hashes it reaches to confirm the trustworthiness of subsequent data it extracts from the proof.
How do you prove it works?
In traditional work on ADSs, the proof that the data structure is secure (i.e., that a malicious server can only successfully lie about its answer with very low probability) is done on a per-data structure basis. This is because the idea behind why ADSs work is embedded in the design of each ADS. Even though this idea is roughly the same for each data structure, the lack of explicitness makes it hard to reason about on its own.
By contrast, the key idea in LambdaAuth is made explicit as a language construct: the semantics of ‘a authtype data and the unauth construct. (Note that there is an auth construct too, for building authenticated data, but we elide that in this post. See the paper for details.) There is a clear connection between what the server does with unauth and what the client does: the server adds the shallow projection of the current value it is considering, while the client consumes that shallow projection and confirms that its hash matches the hash the client expects. We can formalize this connection compositionally without worrying about the other aspects of how the data structure works, since they are the same on both client and server. This design gives us the ability to perform reasoning that works for all data structures (which use authtypes), not just particular ones.
As such, we can prove the following theorem about all LambdaAuth programs: Given a program P that is type correct, and given the client and server versions of that program, PC and PS, respectively, if PS produces a proof that PC consumes successfully, then the answer must be the one that PS would produce when behaving correctly (non-maliciously), with high probability. Type correctness in LambdaAuth boils down to the standard notion of type safety (e.g., don’t use integers as if they were functions), and the proper use of unauth, which is simply that you only pass it values of ‘a authtype, in which case it will produce one of type ‘a.
We can prove this theorem using completely standard, syntactic methods, following how type safety proofs are normally done in programming languages (as detailed, for example, in Benjamin Pierce’s excellent introductory text, Types and Programming Languages). These are the sorts of proofs that graduate students learn in the first few weeks of programming languages courses (e.g., CMSC 631 at Maryland) — they are not hard at all. A feature of such proofs is that they are highly rigorous, e.g., they could be easily mechanized for added assurance, which is great for security applications, and is somewhat in contrast to the more prosaic style of proofs in previous ADS papers.
Conclusions
A takeaway message from this post is that methods developed in the programming languages community, both for formalizing language semantics and for implementing them, are a useful complement to methods used in other areas of computer science, in this case cryptography, where reasoning about computation is important.
To repeat what I said at the start: The key here is that programming language researchers focus on ways of programming (often embodied as language features, patterns, transformations, or analyses), rather than particular programs. As a result, PL results are general-purpose, extending outside of the motivating examples or domain. For LambdaAuth, anyone can now easily create new ADSs, e.g., new datastructures used by bitcoin (our paper has several other examples).
Over time, the PL researcher’s toolbox has filled with useful formal and practical constructs/algorithms/mechanisms that apply to whole languages or ways or programming, and thus support general results, like general-purpose ADS programming and not just particular ADSs, in the case of LambdaAuth described here. I think there is a great opportunity for further collaboration between cryptographers and programming language researchers in particular; I’ll discuss more possibilities in future posts.
More technical details about LambdaAuth can be found in the conference paper and the LambdaAuth web site.