In this post, I’ll continue our ongoing discussion of applications of PL research in computer-assisted education. Specifically, I’ll summarize a talk that Loris D’Antoni of Penn gave at this year’s Workshop on Programming Language Technology for Massive Open Online Courses (PLOOC). I was intrigued by this work, and I think a lot of you may be too.
The AutomataTutor system
In the last post in this series, I talked about how algorithms from PL can be used to develop automated TAs for various high school and college-level courses. Loris and his coauthors have developed such a system, called AutomataTutor, for teaching constructions in undergraduate automata theory.
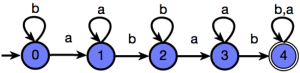
Take a simple automata theory problem: “Draw the deterministic finite automaton (DFA) that accepts the language {s | ‘ab’ appears in s exactly 2 times }.” The correct solution to this problem looks like this:
But suppose, instead of drawing the correct automaton, the student draws an automaton below, which accepts the language of strings where ‘ab’ appears at least 2 times.
Assuming the student has submitted her solution in a formal notation, finding whether the solution is correct is easy: you algorithmically check if the student’s DFA is equivalent to the DFA in the correct solution. But a diligent human TA would go further and find out the mistake that the student made, and give partial credit based on the egregiousness of this mistake. Could we mimic such a TA using an algorithm?
Loris’s approach to a scenario like this is to find the smallest perturbation to the problem statement that would explain the student’s incorrect solution. To do this, he translates the student’s DFA into a formula in monadic second-order logic (MSO): predicate logic where you are allowed to quantify over sets. This translation is grounded in a fundamental mathematical property of finite automata, that every finite automaton can be translated into an equivalent MSO formula. Through this translation, AutomataTutor can essentially recover the specification — the ill-understood problem statement — that the student implemented. Next it finds the minimal edit path between this incorrect specification and the specification that the instructor wanted the student to implement. The greater the length of this path, the bigger the student’s mistake, and so this path gives us a way to score the student’s solution. The path is also a concrete fix to the student’s submission, and AutomataTutor is able to translate it into a natural-language hint that the student can use to correct her work. Specifically, in the above example, AutomataTutor produces a hint along the lines of: “Your solution accepts the following set of strings: {s | ‘ab’ appears in s at least twice}” (the phrase “at least” is in bold because it does not appear in the instructor-defined specification).
In the example above, the student misunderstood the problem statement (the specification). Another possibility is that the student understood the problem perfectly, but the solution had a small bug. In this case, AutomataTutor would search for small sequence of edits to the student’s DFA that would convert it into the correct solution. Edits could be defined in a variety of ways — for example, as a change that makes a final state of the automaton non-final, or the addition of a state. Once again, the length of the edit path could be used to generate a quantitative score for the student’s submission.
AutomataTutor also has a few other algorithmic techniques up its sleeves — for more details, read Loris’s paper “Automated Grading of DFA Constructions”, published at IJCAI 2013.
Aside from all the technical work, Loris and his co-authors did a user study to test the effectiveness of the system. In this study, a set of automata construction problems were graded by AutomataTutor and two human graders. It turned out that the grades that AutomataTutor produced were statistically indistinguishable from the human graders’, and that the tool was closer to each of the humans than the humans were to each other. In the cases where AutomataTutor disagreed with a human, the human grader often realized that his grade was inaccurate.
From automata to programs
AutomataTutor may seem to be restricted to a small class of problems in an upper-level theory course. However, the high-level ideas behind it are also relevant to a broad set of courses, particularly those that involve programming. (This is hardly surprising given that automata are a simple class of programs.) Specifically, mistakes in programming problems can arise from misunderstanding the problem statement or being careless with the implementation. To catch mistakes of the first type, we could, like AutomataTutor, extract a specification out of the student’s program — a logical formula that summarizes what the program actually does. Methods from automated program analysis can be used to generate such a summary. Now we could compare this formula with an instructor-written logical description of the problem that the student was solving. Like in AutomataTutor, we could compute a suitable distance between these two logical descriptions, and use this distance to score the submission and give feedback to the student.
For errors of the second type, we could use AutomataTutor’s strategy of searching for fixes to a student’s program. In fact, the paper “Automated Feedback Generation for Introductory Programming Assignments”, by Rishabh Singh, Sumit Gulwani and Armando Solar-Lezama (PLDI 2013), does this in a comprehensive way, using a program synthesis algorithm to find the simplest way in which a student’s program can be corrected. This fix can be used to give feedback to the student and also to give partial credit.
Technical challenges
These papers open up some fascinating research questions. Most traditional approaches to PL take a binary view of program correctness: a program is either correct or incorrect, with nothing in between. But even the most milquetoast of students would revolt if the only marks that she could receive in an assignment were all or nothing. Thus, educational applications demand tools that can reason quantitatively about the correctness of programs (or automata, or proofs). In particular, they should be able to prove that a program is approximately correct. However, quantitative analysis of programs and proofs is a relatively new field, decades behind boolean verification/analysis of programs.
Secondly, in educational applications, merely scoring a submission isn’t enough — we also ought to give an explanation for the score and feedback about how it can be improved. This amounts to the automatic generation of programs, proofs, and so on, and takes us beyond program analysis to the world of program synthesis, a new discipline at the cutting edge of PL research.
Conclusion
The “tl; dr”? There is much interesting research to be done on PL tools for educational applications. Also, as I said in my last post, these tools have much to contribute to pedagogy, especially when we are talking about teaching at the scale of MOOCs. I hope that more of you consider contributing to this research area.
I’ll end by listing a few other papers/talks that could teach you about this space:
- My friend Sumit Gulwani is a pioneering figure in this research area. (He is a coauthor of the AutomataTutor work as well.) His CACM paper on the use of example-based learning in intelligent tutoring systems is a must-read for anyone interested in PL research for education.
- Benjamin Pierce was one of the first to talk about automated TAs based on PL tools. His upper-level class on Software Foundations uses the Coq theorem prover as a teaching assistant that guides students’ proofs. Check out his ICFP 2009 keynote talk “Lambda, the ultimate TA”.
- At PLOOC, Daniel Perelman gave an excellent talk on the use of automated reasoning in “code puzzles” that teach students how to program. Read Daniel’s paper on this topic.
- In this post, I have primarily talked about automatic grading and generation of feedback for students. Another interesting direction of research is the automatic generation of exam and homework problems. Here are two papers that address this question in the domains of high-school-level geometry and algebra.